La SER monostatique est calculée et comparée aux données mesurées publiées dans l’article suivant : A.C. Woo, H.T.G. Wang, M.J Schuh and M.L Sanders » Benchmark Radar Targets for the Validation of Computational Electromagnetics Programs » IEEE Antennas and Propagation Magazine, Vol. 35, No. 1, February 1993. Ces modèles sont destinés à la validation et à l’étalonnage des logiciels de simulation électromagnétique. Toutes les simulations avec le logiciel CAPITOLE-RCS ont été effectuées sur un ordinateur portable Windows 10 avec Intel core i7 CPU et 16 Gb de mémoire RAM.
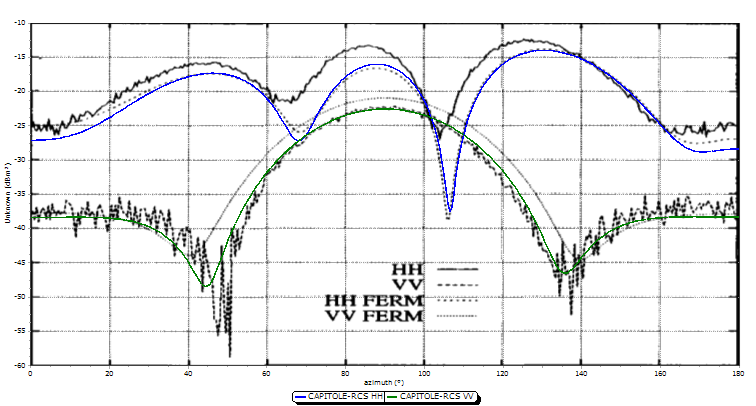
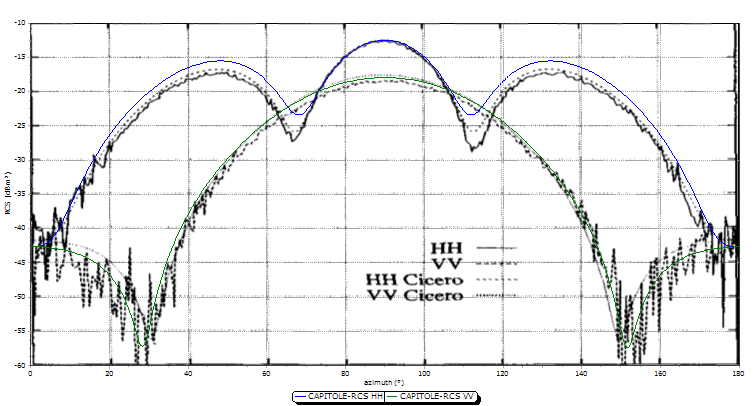
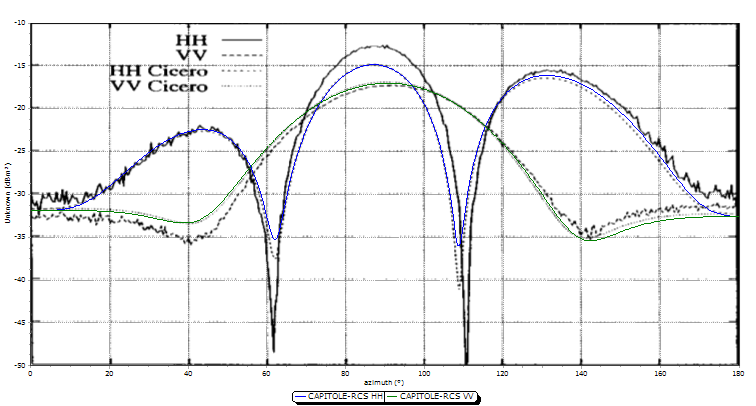
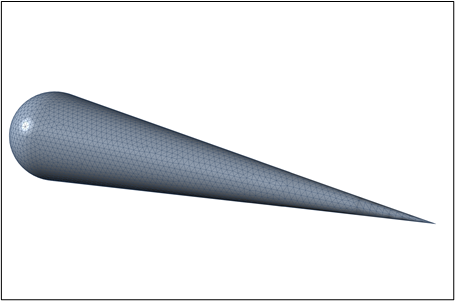
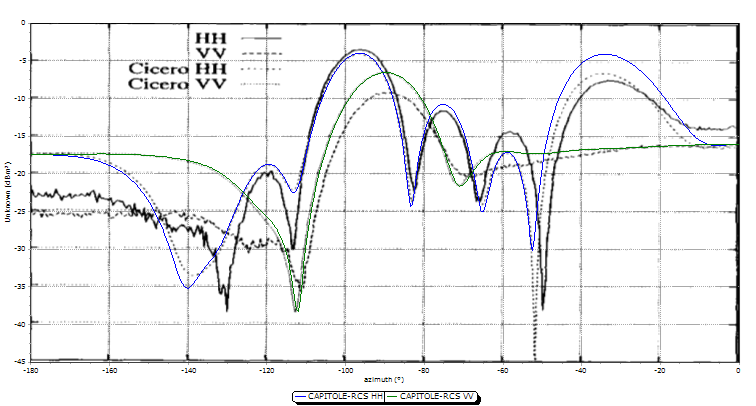
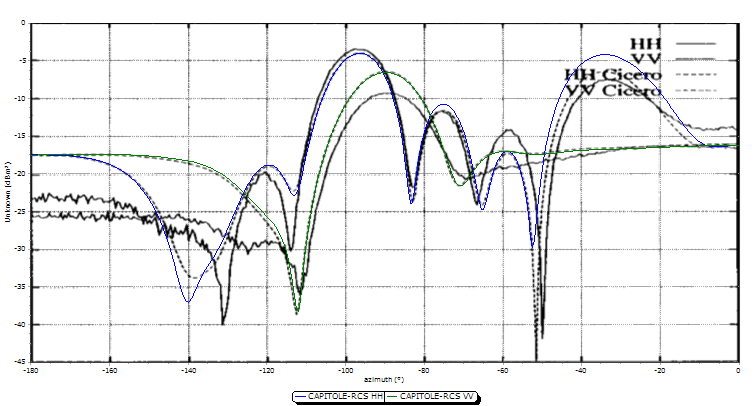
Le « Metallic Almond » n’est en fait pas une forme simple. Elle est définie par des équations mathématiques pour former une surface en forme d’amande. Ce modèle est très intéressant pour l’étude de la SER car il met en évidence une grande dynamique sur la valeur de la SER. Le maillage doit être affiné sur la pointe et la base pour conserver une bonne précision sur les résultats.
La longueur totale est de 0,25 m (9,936 pouces).
La SER monostatique est calculée à 3 fréquences : 1,19, 7 et 9,92 GHz.
Pour la polarisation verticale et horizontale.
La SER est représentée en dBm2 en fonction de l’angle d’azimut de 0 à 180°. L’azimut zéro correspond à l’incidence sur la pointe. L’angle d’élévation est nul.
La méthode du moment a été utilisée avec le solveur MSCBD et les équations EFIE.
| 1.19 GHz | 7 GHz | 9.92 GHz | |
|---|---|---|---|
| Taille des mailles | Lambda/40 | Lambda/15 | Lambda/15 |
| Nombre d'inconnues | 3 546 | 17 262 | 34 692 |
| Durée totale | 2 secondes | 17 secondes | 57 secondes |
Le modèle a été créé à partir de l’expression analytique pour créer une courbe et tourné pour créer une surface. La longueur totale est de 0,254 m (10 pouces).
Paramètres de simulation :
La SER monostatique est calculée à 2 fréquences : 1,18 et 9 GHz.
Pour la polarisation verticale et horizontale.
La SER est représentée en dBm2 en fonction de l’angle d’azimut de 0 à 180°. L’azimut zéro correspond à l’incidence sur la pointe. L’angle d’élévation est nul.
La méthode du moment a été utilisée avec le solveur MSCBD et les équations EFIE.
| 1.18 GHz | 9 GHz | |
|---|---|---|
| Taille des mailles | Lambda/50 | Lambda/20 |
| Nombre d'inconnues | 3 648 | 34 968 |
| Durée totale | 1 seconde | 1 minute et 12 secondes |
Le modèle a été créé à partir de l’expression analytique pour créer une courbe et tourné pour créer une surface.
La longueur totale est de 0,191 m (7,5 pouces).
Paramètres de simulation :
La SER monostatique est calculée à 2 fréquences : 1,57 et 9 GHz.
Pour la polarisation verticale et horizontale.
La SER est représentée en dBm2 en fonction de l’angle d’azimut de 0 à 180°. L’angle d’élévation est nul.
La méthode du moment a été utilisée avec le solveur MSCBD et les équations EFIE.
| 1.57 GHz | 9 GHz | |
|---|---|---|
| Taille des mailles | Lambda/40 | Lambda/15 |
| Nombre d'inconnues | 3 288 | 15 096 |
| Durée totale | 1 seconde | 13 secondes |
Le modèle a été créé à partir de l’expression analytique pour créer une courbe et tourné pour créer une surface.
La longueur totale est de 0,689 m (27,127 pouces).
La SER monostatique est calculée à 2 fréquences : 869 MHz et 9 GHz.
Pour la polarisation verticale et horizontale.
La SER est représentée en dBm2 en fonction de l’angle d’azimut de -180 à 0°. L’azimut de -180 degrés correspond à l’incidence sur la pointe. L’angle d’élévation est de zéro.
La méthode du moment a été utilisée et les équations de l’EFIE ont été utilisées.
| 869 MHz | 9 GHz | |
|---|---|---|
| Taille des mailles | Lambda/40 | Lambda/20 |
| Nombre d'inconnues | 8 664 | 227 793 |
| Durée totale | 12 secondes | 3h11 min (sur un serveur de 48 cœurs) |
Le modèle a été créé à partir de l’expression analytique pour créer une courbe et tourné pour créer une surface.
La longueur totale est de 0,689 m (27,127 pouces).
La SER monostatique est calculée à 2 fréquences : 869 MHz et 9 GHz.
Pour la polarisation verticale et horizontale.
La SER est représentée en dBm2 en fonction de l’angle d’azimut de -180 à 0°. L’azimut de -180° correspond à l’incidence sur la pointe. L’angle d’élévation est de zéro.
La méthode du moment a été utilisée avec le solveur MSCBD et les équations EFIE.
| 869 MHz | 9 GHz | |
|---|---|---|
| Taille des mailles | Lambda/40 | Lambda/15 |
| Nombre d'inconnues | 8 952 | 131 508 |
| Durée totale | 13 secondes | 7 min 26 secondes |
